GEOMETRIA

Caso queira imprimir essa revisão utilize nossa mais nova função: Print, que serve para imprimir as páginas do blog! 

3º BIMESTRE

Cálculo com medianas

A mediana de um triângulo é um segmento que surge no vértice e divide o lado oposto em 2 (neste caso surgiu no vértice C e dividiu o lado AB em dois iguais).
Podemos calcular a medida dos lados utilizando a mediana. Como mostrado abaixo: (clique na imagem)

Calcule o perímetro do triângulo BCE, sabendo que EM é a MEDIANA.

Se EM é a mediana x+3 = 2x-2, pois ela dividiu o lado BC em dois, assim achamos a medida de X:


x+3 = 2x - 2
x + 3 + 2 = 2x
3+2 = 2x - x
5 = x
 E assim substituímos x por 5, e somamos, dando o perímetro do triângulo, que é 35.

Casos de congruência

• Caso lado-ângulo-lado:  

Quando dois triângulos tem dois lados congruentes e que esses dois lados formem um angulo congruente.

• Caso lado-lado-lado:

Quando dois triângulos tem os três lados congruentes.

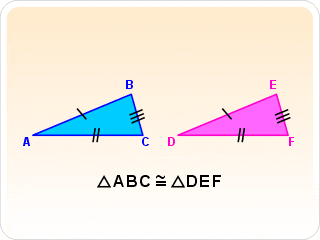
• Caso ângulo lado ângulo:

Se dois triângulos possuem um lado congruente e os dois ângulos formados por esse lado também forem congruentes.

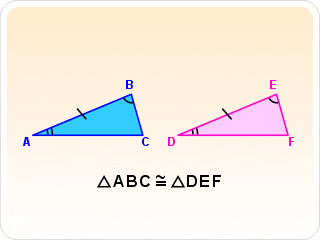
• Caso lado-angulo-angulo oposto:

Se tem dois triangulos com um lado , um angulo e um angulo oposto a esse lado congruentes.

Figuras geométricas não planas (3D).

Corpos redondos

Prismas
Tem duas bases paralelas congruentes:

Piramides
tem uma base poligonal e um vértice:

Secções de figuras não planas:
 Se as figuras não planas forem cortadas se obtêm figuras planas, observe:

                                             VERTICAL                                                            HORIZONTAL














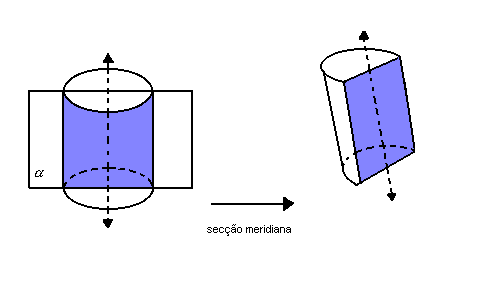
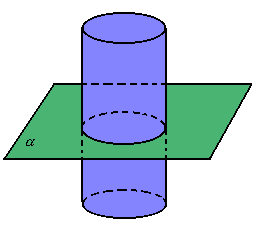
No cilindro cortando na horizontal forma um círculo, porém, se cortar na vertical, forma um retângulo.

Planificação

Quando desenhamos as figuras "abertas" numa superfície plana.

Na planificação do paralelepípedo acima obtivemos 4 retângulos e 2 quadrados.

Quadriláteros

Todo polígono de 4 lados.

Veja abaixo outra denominações:

Quadriláteros CONVEXOS ou NÃO CONVEXOS

Soma das medidas dos ângulos (Si) de um quadrilátero Convexo

A + B+ C+ D = 360º

aplica-se á todos os quadriláteros convexos.









Paralelogramos


Quadrilátero com lados opostos paralelos.







Classificação dos paralelogramos

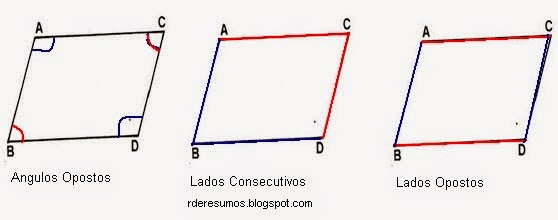
Propriedades dos paralelogramos

As diagonais são congruentes e cruzam-se no meio.
Os lados opostos são congruentes.
Os ângulos opostos são congruentes
Os ângulos consecutivos são suplementares (180º)


ATIVIDADES

FIM

Polígonos:

Diagonal de um polígono:

É um segmento que tem suas extremidades em 2 vértices não consecutivos( que não estão um do lado do outro).
O triângulo não possui diagonais. Para achar o número de diagonais de polígono qualquer usamos a seguinte fórmula:
             d =  n . (n-3)                  n = números de lados
                         2                       d = diagonais

Soma dos ângulos internos (Si):

Em qualquer triângulo a soma dos ângulos internos é 180º

Podemos achar x nessa figura, através dessa teoria:

40 + 70 + x = 180

110 + x = 180

x = 180 - 110

x = 70º

Podemos também achar a soma dos ângulos internos de outro polígono, com a seguinte fórmula:

Si = (n-2) . 180

Podemos  ter um exemplo:

esse decágono é um polígono regular(todos os lados e ângulos iguais), nele podemos achar o valor de cada ângulo que vamos denominar de x. Primeiramente temos que achar a soma dos ângulos internos usando a fórmula.

(10 - 2) . 180

8 . 180 

1440º

Quando acharmos a soma dos ângulos internos do polígono regular, dividimos pelo número de lados, para obter o valor de cada ângulo X.

 1440   =  144º

   10     

Podemos concluir que cada ângulo do decágono mede 144º 

Mas se o polígona NÃO FOR REGULAR?

Para achar x temos que primeiro achar a soma dos ângulos internos do polígono.

(4-2) . 180

2 . 180

360º

Aplicando a fórmula vimos que a soma dos ângulos internos do quadrilátero acima é 360º, e para achar o valor de x devemos somar todos os ângulos igual a 360º.

50 + 70 + 110 + x = 360

230 + x = 360

x = 360 - 230

x = 130º

Triângulos:

Teoria do ângulo externo: O ângulo externo é igual a soma dos dois ângulos internos.

Neste caso d = a + c

Podemos observar abaixo outro caso em que podemos aplicar essa teoria:

 Para achar o valor de X devemos somar os 2 outros ângulos de dentro.

X = 30 + 75

X = 105

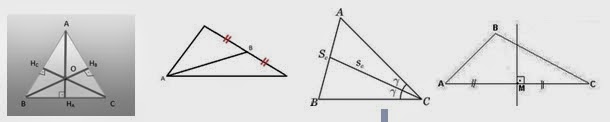
Pontos notáveis de um triângulo:

• Medianas: Segmentos que surgem do vértice e divide o lado oposto em 2 iguais.
• Baricentro: Ponto de encontro das medianas.

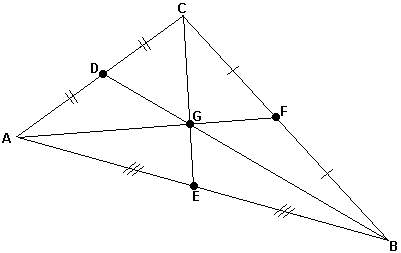  Neste caso D, E e F são medianas e G é o baricentro.

• Altura: Segmento que surge no vértice e forma um ângulo reto com o lado oposto.
• Ortocentro: Ponto de encontro das alturas

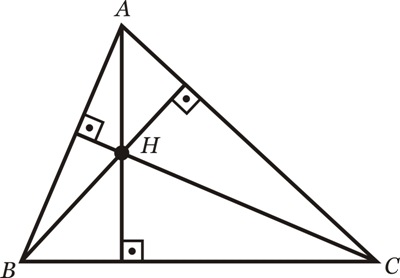  Neste caso A, B e C são as alturas e H é o ortocentro.

• Bissetriz: Segmento que surge do vértice e divide o ângulo em 2 iguais.
• Incentro: Ponto de encontro das bissetrizes.

Neste caso P, N e M são as bissetrizes, e I é o incentro.

• Mediatriz: Divide o lado em 2, porém não surge do vértice e forma um ângulo de 90º com o lado oposto.
• Circuncentro: Ponto de encontro das mediatrizes.

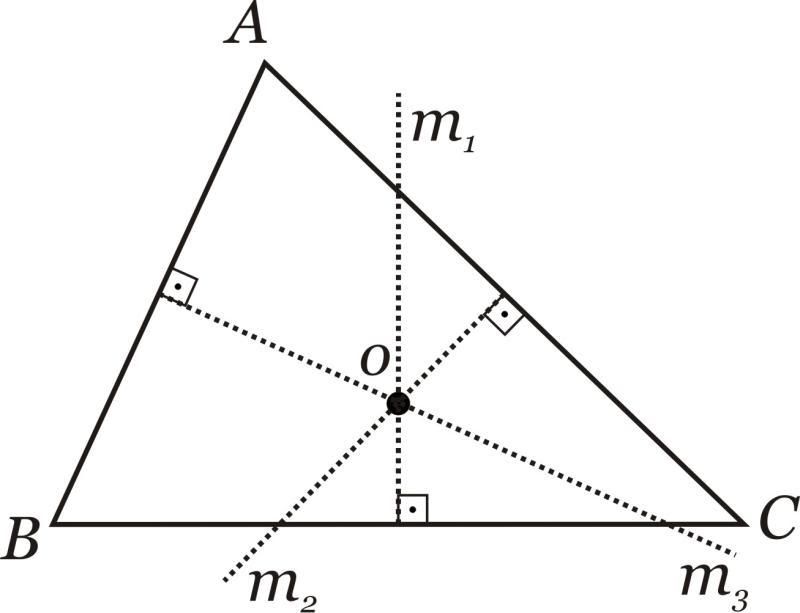  Neste caso m¹, m² e m³ são as mediatrizes, e O é o circuncentro.

ATIVIDADES: (REVISÃO DE GEOMETRIA PASSADA PELA PATRÍCIA)

EXERCÍCIOS

1)   Utilizando a fórmula que estudamos em sala,determine o número de DIAGONAIS dos seguintes polígonos.                                                                                                                                       

a)Icoságono

b) Eneágono

2.Considere um polígono de 12 lados e responda:

a)    Qual é o seu nome?_______________________________________________________

b)    Quanto mede a soma de seus ângulos internos?

c)    Quantas diagonais ele tem?

3.Calcule o valor de x nas figuras abaixo, mas lembre-se que antes é necessário calcular a medida da soma de seus ângulos internos

4.Os ângulos de um triângulo são expres­sos por 3x + 5°, 4x + 10° e 6x – 30°. Qual é o valor de cada ângulo?

7. Considere os pontos notáveis de um triângulo, sendo: B  Baricentro; C  Circuncentro; I Incentro; O Ortocentro.

 (    ) Ponto de encontro das medianas.

 (    ) Ponto de encontro das mediatrizes dos lados de um triângulo.

 (    ) Ponto de encontro das bissetrizes internas de um triângulo

 (    ) Ponto de encontro das retas suportes das alturas.

8. Marque as afirmações a seguir com ver­dadeiro (V) ou falso (F).

(    ) O ponto de encontro das medianas de um triângulo é chamado baricentro.

(    ) O ponto de encontro das retas su­portes das alturas de um triângulo é chama­do incentro.

(    ) O ponto de encontro das bissetrizes de um triângulo é chamado incentro.

(    ) O ponto de encontro das mediatrizes dos lados de um triângulo é chamado bari­centro.

9. Observe as figuras a seguir e escreva o nome de cada um dos segmentos.

Clique aqui para ver o gabarito.